Centered pentagonal number

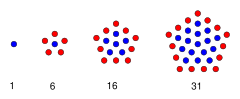
In mathematics, a centered pentagonal number is a centered figurate number that represents a pentagon with a dot in the center and all other dots surrounding the center in successive pentagonal layers. The centered pentagonal number for n is given by the formula

$P_{n}={{5n^{2}-5n+2} \over 2},n\geq 1$

The first few centered pentagonal numbers are

1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951, 1051, 1156, 1266, 1381, 1501, 1626, 1756, 1891, 2031, 2176, 2326, 2481, 2641, 2806, 2976 (sequence A005891 in the OEIS).

Properties

• The parity of centered pentagonal numbers follows the pattern odd-even-even-odd, and in base 10 the units follow the pattern 1-6-6-1.
• Centered pentagonal numbers follow the following recurrence relations:

$P_{n}=P_{n-1}+5n,P_{0}=1$

$P_{n}=3(P_{n-1}-P_{n-2})+P_{n-3},P_{0}=1,P_{1}=6,P_{2}=16$

• Centered pentagonal numbers can be expressed using triangular numbers:

$P_{n}=5T_{n-1}+1$

See also

• Pentagonal number
• Polygonal number
• Centered polygonal number

External links

• Weisstein, Eric W. "Centered pentagonal number". MathWorld.